Pada Pembelajaran Matematika Bab Transformasi, maka kita akan membahas empat Jenis transformasi yaitu Translasi (Pergeseran), Refleksi (Pencerminan), Rotasi (Perputaran), dan Dilatasi (Perkalian). Nah Untuk dapat memahami konsep transformasi tersebut dengan mudah, maka kita perlu membahasnya satu persatu.
Langsung saja tanpa basa-basi lagi, mari kita mulai pelajari ke-4 jenis transformasi tersebut, Namun untuk kesempatan kali ini, kita akan fokus membahas Translasi terlebih dulu ya.
Translasi / Pergeseran

Gambar di di atas, menunjukkan seorang anak sedang bermain prosotan. Panjang landasan prosotan tersebut adalah 4 meter. Ia meluncur mulai dari bagian atas prosotan sampai ke bagian bawah dengan kemiringan atau arah mengikuti permukaan landasan prosotan. Dari situasi tersebut, dapatkah kalian menentukan jauhnya jarak pergeseran yang ditempuh oleh anak tersebut? Bagaimana arah pergeseran masing-masing anggota tubuh anak tersebut selama berseluncur?
Pengertian Translasi
Perhatikan Gambar dibawah ini dulu ya

Pada translasi tersebut, diperoleh hubungan-hubungan berikut:
AB → A’B’ (dibaca: AB menempati A’B’), maka AB = A’B’ dan AB // A’B’,AD → A’D , maka AD = A’D’ dan AD // A’D’,
Segi empat ABCD → segi empat A’B’C’D , maka segi empat ABCD kongruen atau sama dan sebangun dengan segi empat A’B’C’D .
Translasi (pergeseran) adalah suatu perpindahan semua titik pada suatu bodang (datar) dengan jarak (besar) dan arah yang sama. Suatu translasi dapat diwakili oleh sebuah ruas garis berarah. {alertInfo}
Contoh Soal
Gambarlah persegi panjang EFGH dan bayangannya pada translasi (pergeseran) yang diwakili oleh !
- Bagaimana hubungan sisi GF dan bayangannya?
- Bagaimana hubungan bangun EFGH dan bayangannya?
Jawab:
Gambarlah persegi panjang EFGH, kemudian tentukan bayangannya dengan cara membuat .
- Bayangan dari adalah Panjang dan .
- Bangun dan bayangannya yaitu bangunkongruen atau sama dan sebangun.
{alertSuccess}
Notasi Translasi dengan Pasangan Bilangan
Suatu translasi, selain dapat diwakili oleh sebuah ruas garis berarah, dapat juga dinyatakan dengan pasangan bilangan dengan x sebagai komponen mendatar (horizontal) dan y sebagai komponen tegak (vertikal).
Baca Juga : Soal Ulangan Harian Pola Bilangan Kelas 8{alertWarning}
Translasi (a/b) memindahkan titik dengan aturan berikut:
- a satuan mandatar ke kanan jika posisi a positif atau a satuan ke kiri jika a negatif.
- b satuan tegak ke atas jika b positif atau b satuan ke bawah jika b negatif.
Koordinat Bayangan

Gambar di diatas menunjukkan titik A(–6, 5) digeser 10 satuan ke kanan, kemudian digeser lagi 8 satuan ke bawah.
Untuk mempermudah pemahaman, situasi tersebut dapat dinyatakan dengan cara berikut.

Contoh Soal
A(8, 3), B(5, –3), dan C(10, –2) adalah titik sudut pada ΔABC. Pada translasi , Δ ABC dipetakan ke Δ A’B’C’.
- Gambarlah ΔABC beserta bayangannya!
- Tentukan koordinat titik A’, B’, dan C’!
Jawab:
{alertSuccess}
- Lihat gambar di dibawah
- Translasi
Bayangan dari titik A(8, 3) adalah A (8 + (–8), 3 + 1),
maka A (0, 4).
Bayangan dari titik B(5, –3) adalah B (5 + (–8), –3 + 1), maka B (–3, –2).
Bayangan dari titik C(10, –2) adalah C (10 + (–8), –2 + 1), maka C (2, –1).
Dua Translasi Berurutan
Perhatikan gambar di bawah. mewakili translasi dan mewakili translasi .
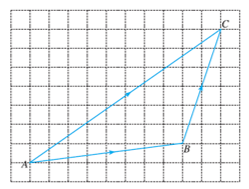
Hubungan komponen dan terhadap komponen dapat dinyatakan dengan cara berikut.
⊕ mewakili ⊕ .
Dengan demikian, dapat disimpulkan sebagai berikut.
Untuk dua translasi berurutan (a/b) dan (c/d) berlaku: (a/b) + (c/d) = (a+c/b+d){alertSuccess}
Terimakasih Kamu sudah membaca Tulisan kami mengenai Memahami Konsep Transformasi dengan Mudah. Semoga Bermanfaat dan jangan lupa bagikan artikel ini dengan klik link berbagi dibawah ini.



